چکیده

در این مقاله نحوه استفاده از اشکال هندسی در معماری از طریق بیان چندین مثال مورد بحث و بررسی قرار گرفته است. هندسه علم بنیادین فرم ها و نظم موجود در آن هاست. اشکال هندسی، فرم ها و تغییر شکل ها بدنه اصلی طراحی معماری را شکل می دهند. درتاریخچه معماری، قواعد هندسی براساس نظریه های تناسب و تقارن، ابزار معینی را برای طراحی معماری شکل داده اند. تناسبات در طبیعت مورد تجزیه و تحلیل قرار گرفت و به عنوان جنبه اصلی زیبایی شناختی در طبیعت و هنر مطرح گردید. بنابراین تناسباتی مانند نسبت طلایی به عنوان عاملی قدرتمند برای ایجاد هماهنگی و هارمونی در معماری و همچنین هنر و موسیقی مدنظر قرارگرفت. براساس نظریه فیثاغورس قواعدی کلی برای هارمونی و هماهنگی وجود دارد. این قواعد در معماری نیز به کار گرفته شده و خصوصا در دوره رنسانس پیشرفتهای بیشتری داشته اند. لئون بتیستا آلبرتی این قواعد کلی حاکم برتناسبات هارمونیک را درتئوری معماری خود ادغام کرده و در ساخته هایش به کار برده است. یافتن اصول کلی هارمونی حاکم بر جهان، هدف اصلی تحقیقاتی یوهانس کپلر در کتاب “هارمونی در جهان” می باشد. این اصول و قواعد هارمونیک بر پایه علم هندسه استوار هستند. شاخه مهم دیگر در پیشینه اصول طراحی معماری “نسبت طلایی” یا “تناسب مقدس” می باشد.”شبکه مدولار” لوکوربوزیه نمونه ای از طراحی معماری و شکل گیری کانسپت بر مبنای نسبت طلایی می باشد. مفهوم تقارن با ایده هارمونی و تناسب ترکیب شده است. عملکردهای متقارن به نحوه حرکت فرم ها و اشکال مرتبط هستند. علاوه بر این هندسه می تواند به عنوان علمی ساختاری قلمداد شود. طراحی معماری بر مبنای ساختارهای هندسی با استفاده از تبدیلات و تغییر شکل ها شکل گرفته است. استفاده از تبدیلات و تغییر شکل های متقارن به عنوان کانسپت طراحی به خوبی در تاریخچه معماری قابل ملاحظه است. در معماری معاصر هیچ قانون ثابتی در مورد کانسپت های طراحی وجود ندارد. اما همچنان ارتباطاتی با مفاهیم فضایی هندسی برقرار است. لازم است که یک پیشینه هندسی بروز برای طرح معماری تهیه شود. در این مقاله نمونه هایی در زمینه معماری و طراحی ارائه شده و ارتباط آن ها با مسئله کاربرد هندسه و اشکال هندسی در معماری مورد بررسی قرار می گیرد. و همچنین نقش هندسه در فرآیندهای طراحی معماری به دقت از طریق بررسی تاریخچه معماری و رویکردهای نوین و نتیجه بخش، مورد تجزیه و تحلیل قرار می گیرد و در نهایت دیدگاه هایی جدید و حقیقی ارائه خواهد شد.

کلمات کلیدی: ساختارهای هندسی، هارمونی، تناسبات، طراحی معماری، اشکال هندسی در معماری

1. مقدمه

می توان گفت علم بنیادین فرم ها و نظم هندسی موجود در آن ها وارد پروسه ساخت و طراحی معماری شده است. ساخت یک اثر معماری با المان ها و ارتباطات میان آن ها آغاز می گردد. هندسه می تواند بر این روند از طریق تعامل با فرم ها و اشکال هندسی به عنوان المان های اصلی در این پروسه و همچنین تناسبات، زوایا و تغییر شکل ها به عنوان ارتباطات موجود میان المان های مطرح شده، تاثیرگذار باشد. ساختارها و سازه ها اساس و پایه پروسه ساخت را شکل می دهند. سازه ها در واقع سیستم های کلی نظم دهنده ای هستند که از اصول علمی متنوعی پیروی می کنند. سازه از لغت لاتین “structura” به معنی مجموعه ای منظم مشتق شده است. ریاضیات می تواند به عنوان پایه علمی ساختارها و سازه ها مطرح گردد. ریاضیات سیستم های عناصر و ارتباطات و عملکرد آن ها را در نظر می گیرد. این کانسپت به عنوان مثال پایه و اساس رویکرد خلاقانه ای است که ریچارد باکمینیستر فولر در آثار خود به کار می گیرد. “به طور کلی ریاضیات علم سازه و الگوست.” [۷]

تصویر ۱: ریچارد باکمینیستر فولر و مدل های ساخته شده، ۱۹۴۹

به عنوان مثال او در تحقیقاتش روشی سیستماتیک برای تقسیم سطح یک کره معرفی نمود. او با طرز تفکر سازه ای خود و با در نظر گرفتن احجام افلاطونی، ایده شبکه های ژئودزیک را مطرح کرد که در نهایت به ساخت گنبدهای ژئودزیک انجامید. هندسه می تواند به عنوان علمی که نحوه عملکرد سازه ها را توضیح می دهد مطرح گردد. مکس بیل با هنرمندی بر روی ساختارهای هندسی به عنوان دستورالعمل های قابل استفاده کار کرد. به عنوان مثال برای ایجاد تغییر در یک موضوع خاص، یعنی پروسه تبدیل مثلث به هشت ضلعی. او توانست با ایجاد گزینه های متنوع، روش های مورد استفاده خود را برای تولید آثار هنری به وضوح بیان کند.

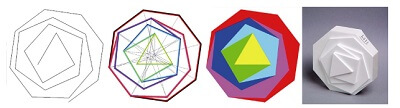تصویر ۲: مکس بیل، ۱۹۳۸-۱۹۳۵، روند تغییر شکل از مثلث به هشت ضلعی

مکس بیل در مورد ارتباط میان سازه ها و هنر اندیشید. بر اساس نظریه او نظمی ریتمیک به عنوان عاملی برای ایجاد خلاقیت می تواند توسط معمار برای تولید یک اثر هنری به خدمت گرفته شود. اثری که از یک ساختار کلی آغاز شده است. در تاریخچه علم هندسه و کاربرد اشکال هندسی در معماری، قوانین هندسی شکل گرفته است که پایه و اساس ساخت آثار معماری را شکل می دهند. در متن پیش رو ما به ارزیابی نقش هندسه در پروسه های طراحی معماری از طریق بیان چندین نمونه در تاریخچه معماری می پردازیم.

2. هارمونی به عنوان یک اصل در روند شکل گیری یک اثر هنری

مفهوم هارمونی به عنوان یک اصل بنیادین در شکل گیری آثار هنری در تاریخچه معماری مطرح است. تولید آثار هنری بر اساس هماهنگی، هارمونی و نظم به عنوان مباحث مرتبط با مقوله زیبایی شناختی صورت می گیرد. مفهوم هارمونی بر اساس یک افسانه شکل گرفت “هارمونیا”، خدای هماهنگی و نظم که دختر آرس، خدای جنگ و افرودیت، خدای عشق و زیبایی است. هارمونیا نمادی از اجتماع نقیضین است. هارمونی به معنای ایجاد ارتباط میان موضوعات متفاوت و متضاد به منظور دستیابی به یک حالت کلی منظم می باشد. اصول نظم و هارمونی در علوم باستانی نیز به چشم می خورد.

• فیثاغورس

در دیدگاه فیثاغورس تمام رویدادها تحت تاثیر اصولی کلی رخ می دهند. یک اصل می تواند در شکل گیری یک اثر هنری مطرح گردد اگر نظم موجود در قواعد ریاضی را در نظر داشته باشد. حساب، هندسه، ستاره شناسی و موسیقی، علوم چهارگانه ای هستند که کاملا برمبنای قواعد کلی فوق الذکر شکل گرفته اند. فیثاغورس متقاعد شده بود که هارمونی و تمام موضوعات و اصول موجود در جهان هستی می تواند از طریق اعداد و قواعد ریاضی به خوبی درک شود. او کشف کرد که فاصله موجود میان نت های موسیقی ارتباطات ساده ای را بر اساس تقسیمات تارها و تعداد نوسانات شکل می دهد. بر اساس نظریه فیثاغورس، تتراکتیس: اعداد ۱ تا ۴ (۴ المان، ۴ نقطه اصلی) شالوده و اساس این ارتباطات را تشکیل می دهد. ایده تناسبات هارمونیک، اصلی کلی برای تمام علوم نظری و کاربردی است.

• آلبرتی

با نگاه به مفهوم کلاسیک هارمونی به عنوان اجتماعی از اضداد، لئون باتیستا آلبرتی (۱۴۷۲-۱۴۰۴) قواعدی را در زمینه معماری مطرح کرد. کتاب “هنر ساختن”[۱] در ده جلد به توضیح این مطلب می پردازد که چگونه می توان به هارمونی در معماری دست یافت. زیبایی از نظر آلبرتی “هماهنگی تمام قسمت ها نسبت به یکدیگر” است و به همین ترتیب بر اساس نظریه های فیثاغورس “این هماهنگی در اعداد، تناسبات و نظمی خاص یافت می شود که برای دستیابی به هارمونی به آن نیاز خواهیم داشت.” نظریه های آلبرتی به عنوان دستورالعملی کلاسیک در معماری از قرن شانزدهم تا هجدهم و حتی پس از آن مطرح بود.

• کپلر

هارمونی به عنوان مفهومی که در تمامی علوم و در سراسر جهان مطرح است، در کتاب “هارمونی در جهان” اثر یوهانس کپلر نیز بیان شده است. یوهانس کپلر (۱۶۳۰-۱۵۷۱) که یک دانشمند، ستاره شناس و ریاضی دان مشهور می باشد، مفهوم هارمونی را بر اساس هندسه، خصوصا احجام افلاطونی بیان می کند. او یکی از پیروان مکتب فیثاغورس بود و ارتباطات ریاضی را پایه و اساس طبیعت و تمام مخلوقات می دانست. مفاهیم هندسی در تئوری او به عنوان پایه و اساس طبیعت و علوم و همچنین هنر و موسیقی مطرح هستند.

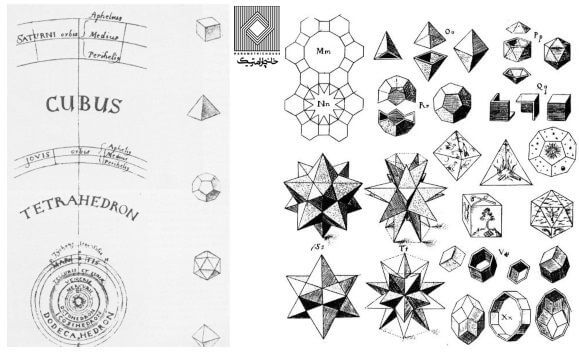تصویر ۳: برگرفته از کتاب “هارمونی در جهان” کپلر

بنابراین ساختن و طراحی نیز بر اساس مفهوم جهان هندسی صورت می گیرد.

• نسبت طلایی

اصول بنیادین هارمونی که از طبیعت نشات گرفته و در هنر، معماری و موسیقی به کار برده می شوند، به خوبی در نسبت طلایی قابل مشاهده هستند. مفهوم نسبت طلایی نشان دهنده سازگاری دو مبحث طراحی و هندسه می باشد. این ایده مدت زمانی طولانی است که وارد حوزه معماری شده است. هیپاسوس (۴۵۰ پیش از میلاد مسیح) در تحقیقات خود درباره پنج ضلعی و ارتباط میان طول اضلاع و قطرهای آن، این نسبت را کشف کرد. اقلیدس (۲۷۰-۳۲۵ پیش از میلاد مسیح) اولین کسی بود که نسبت طلایی را دقیق و کامل به عنوان نسبت موجود در دنباله ای از اعداد توضیح داد. پس از او نسبت طلایی به عنوان تناسبی ایده آل و کامل در مباحث زیبایی شناختی و هارمونی مطرح گردید. خصوصا در دوره رنسانس، تناسبات هارمونیک بر مبنای ارتباطات هندسی متناسب با نسبت طلایی در هنر، معماری و همچنین موسیقی مورد توجه قرار گرفت. فلیپو برونلسکی کلیسای سانتاماریا دلفیوره را در سال ۱۲۹۶ بر اساس نسبت طلایی و دنباله اعداد فیبوناچی ساخت.

با وجود این که”شبکه مدولار” لوکوربوزیه[۵] نمونه ای از یک کانسپت آرکی تکتونیک در زمینه طراحی و ساخت بر مبنای قواعد هندسی در معماری مدرن است، اما همچنان به مفهوم کلاسیک هارمونی متعهد باقی مانده است.

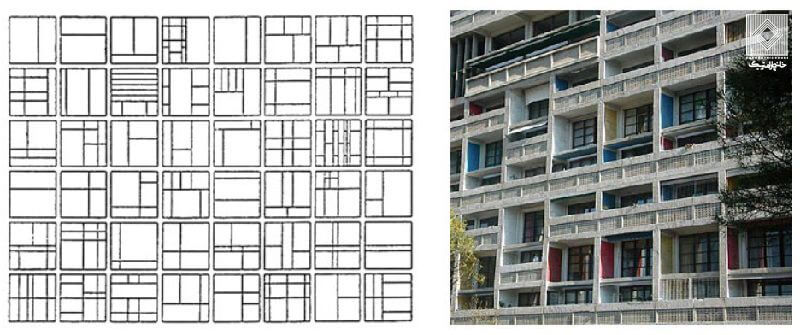تصویر ۴: “بازی های تخته ای” و “ساختمان مسکونی” اثر لوکوربوزیه

ساختاربندی پنجره ها در ساختمان مسکونی، در شهر مارسی، سال ۱۹۴۷ (تصویر ۴) انواع مختلف پیکربندی را با حفظ قواعد سازه ای موجود نشان می دهد که بر اساس نسبت طلایی تقسیم بندی شده اند. یک تشابه ساختاری میان موسیقی و معماری، در امواج به کار رفته در ساخت موسیقی “Metastasi” توسط “Xenakis”و نمای صومعه”La Tourette” اثر لوکوربوزیه/ Xenakis در سال ۱۹۵۲ به وضوح دیده می شود[۱۱]. پل وی. ناردی-رینر در کتاب خود با عنوان “معماری و هارمونی”[۱۳] رابطه میان معماری و هندسه را مشخص می کند: هندسه نقشی بسیار مهم در معماری در پروسه فرمیابی و تکمیل آن بر عهده دارد بدون این که معماری را منحصرا تعریف نماید.

3. تقارن و تغییر شکل

یک مفهوم بنیادین دیگر در تاریخچه معماری کانسپت تقارن است که ارتباطی تنگاتنگ با مفهوم هارمونی دارد. واژه تقارن “Symmetry” که از لغت یونانی “syn” به معنی با هم و لغت “metron” به معنی اندازه گیری، گرفته شده است، در کل به معنی هارمونی و هماهنگی میان اجزاء یک شیء و روش ترکیب چندین بخش می باشد. ویتراو [۱۵] تقارن را به عنوان بخشی مهم از معماری توضیح می دهد. در مفهوم ابتدایی که مد نظر ویتراو بود، تقارن بیان کننده نحوه ترکیب اجزاء به سبکی کلی است و نه روشی محاسباتی و ریاضی.

مفهوم ریاضی مقوله تقارن که امروزه مطرح می شود اولین بار در متون کریستال شناسی ایجاد شد. تنها در اواسط قرن نوزدهم میلادی ریاضی دانان به مفهوم تقارن علاقه مند شدند. بعدها با مطرح شدن مفهوم تبدیل و تغییر شکل در ریاضیات، مفهوم تقارن تغییر کرده و گسترش یافت. در “برنامه Erlangen”، در سال ۱۸۷۲، فلیکس کلین هندسه را به عنوان اصول حاکم بر اجزاء نامتغیر گروه های تبدیل مطرح کرد. اکنون تقارن به عنوان یک نامتغیر در نوع خاصی از تبدیلات بیان می شود [۱۴].

تصویر ۵: تزئینات بر اساس سلسله مراتبی از تبدیلات متشابه

تصویر ۵ تولید یک الگو با استفاده از تبدیلات متشابه را توسط یک دانشجو (مارکوس وایزنمایر) نشان می دهد. دانشجویان میبایست المانی اولیه انتخاب می کردند و سپس سلسله مراتبی از تبدیلات متشابه را بر روی آن اعمال کرده، روند انجام شده را نمایش دهند. سپس روند انجام شده با المان اولیه دیگری مجددا شکل می گیرد. این تکلیف ساده سعی دارد درکی از تفکر ساختارمند ارائه دهد.

پروسه تبدیلات متشابه می تواند به روشی بسیار قابل درک بیان گردد، عمل تا زدن “folding” و برش. تا زدن روشی با اهمیت در فرآیندهای ساخت و تولید در معماری و همچنین صنعت می باشد. پژوهشی در زمینه شرایط تقارن هندسی در فرآیند تا زدن توسط یک دانشجوی معماری (اریک پیگت) [۱۲] و یک نمونه اوریگامی صنعتی [۱۷] در تصویر ۶ نشان داده شده است. درک ریاضی از مقوله تقارن به عنوان فرآیندی تبدیلی، امروزه به منظور تحت تاثیر قرار دادن پروسه های طراحی در معماری مطرح شده است.

تصویر ۶: مطالعات در زمینه فولدینگ و اوریگامی صنعتی

4. کانسپت های فضایی هندسی و معماری

فضای معماری بر اساس یک کانسپت فضایی هندسی شکل می گیرد. خصوصا در پروسه طراحی، معماری در ارتباط با فضای هندسی تعریف می شود. رابین ایوانز [۶] رابطه میان هندسه و معماری را مورد تجزیه و تحلیل قرار می دهد: “اولین مکانی که همه برای یافتن اشکال هندسی در معماری به آن توجه می کنند، فرم ساختمان است، سپس احتمالا فرم های هندسی در طرح ها و نقشه های ساختمان مورد توجه قرار می گیرد. این ها مکان هایی هستند که هندسه به طور کلی در آن ها بسیار ساکن و بی روح است. اما هندسه به صورت فعالی در میان فضاهای ذکر شده و فراتر از آن ها وجود دارد”[۶].

همان طور که ایوانز اشاره می کند، در تاریخچه معماری شما می توانید باورهای غلطی که از نقش هندسه و اشکال هندسی در معماری وجود دارد بیابید. او در مطالعات تاریخی خود او به ارتباطات موجود میان نظریه هندسه ترسیمی گاسپارد مانگ و تئوری معماری جان نیکولاس لوئیس دوراند اشاره می کند. دوراند در اواخر قرن هجدهم و اوایل قرن نوزدهم به تدریس معماری در موسسه École Polytechnique در پاریس به طور هم زمان با مانگ می پرداخت. دوراند یک شبکه طراحی جهانی برای معماری تعریف کرد. اوانز توضیح می دهد که شبکه معماری دوراند (همان طور که در تصویر ۷ مشاهده می کنید) بر اساس برداشتی غلط از سیستم مختصات فضایی شکل گرفته است. به جای درک درست سیستم مختصات با روشی انتزاعی، او صفحات مختصات را مستقیما در معماری به عنوان کف و دیوارها به کار برد.

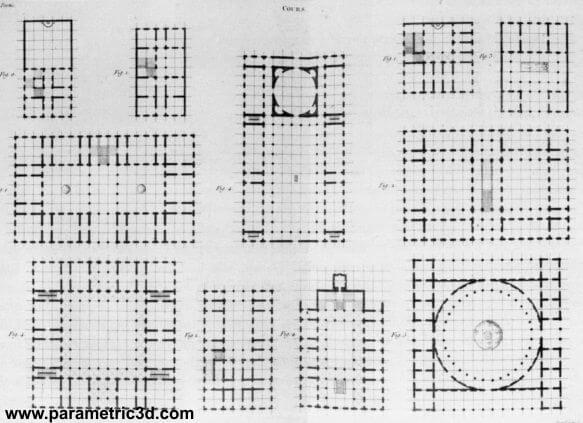تصویر ۷: شبکه معماری دوراند، حیاط ها

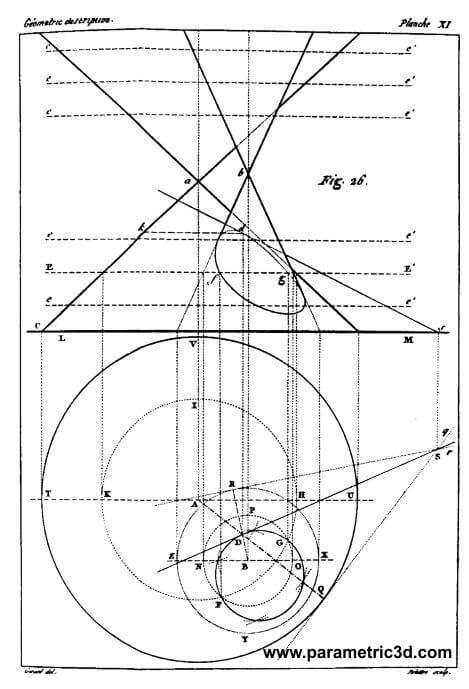تصویر ۸: تصویری از تقاطع دو مخروط، مانگ

به طور هم زمان ریاضی دانان توانستند منحنی ها و سطوح منحنی شکل را با کمک سیستم مختصات خلق کنند.

“… در حالی که هندسه ترسیمی، جهت گیری آزاد فرم ها در رابطه با یکدیگر را ممکن می ساخت، تصویرسازی قائم دوراند به منظور ایجاد جهت گیری های روبرو و مستقیم الخط مورد استفاده قرار می گرفت. بنابراین هرگونه نقص و خطایی که در آموزه های دوراند وجود دارد، مانگ و نظریه های هندسی او نقشی در آن نداشته اند.” [۶, p.327]. امروزه نیز این باور غلط درباره نقش هندسه و اشکال هندسی در معماری وجود دارد اگر فرم های صلب، فرمی هندسی قلمداد شوند و فرم های ارگانیک در تضاد با قوانین هندسی تعریف گردند. اوانز به درستی در کتاب خود بیان می کند: زمانی که معمار تلاش می کند تا از قیود هندسی به معنای چارچوبی که بر آثار دیکته می شود، رهایی یابد. چه جایگزینی خواهد داشت؟ او یا باید به کلی هندسه را کنار بگذارد (که این امر به شدت دشوار است)، یا این که باید گونه دیگری از هندسه را برگزیند که همیشه پیچیده تر و دشوارتر خواهد بود، و یا این که به گونه ای نوع دوم را به کار برد که این تصور ایجاد شود که از نوع اول استفاده کرده است… [۶, p.331].

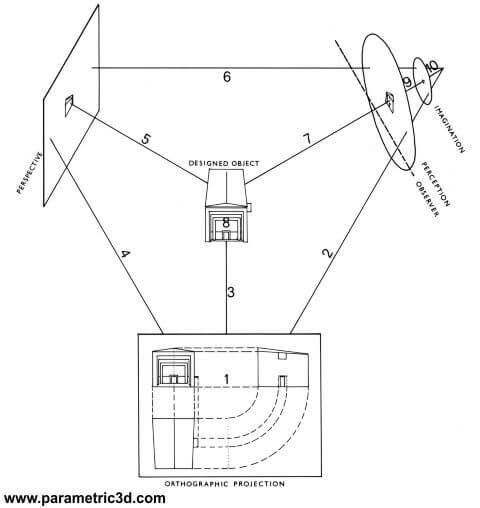
ارائه فهرستی از فرم های صریح و روشن برای معماری مسئله ای مرتبط با علم هندسه نیست. علم هندسه اغلب درکی هندسی از فضا به عنوان پیش زمینه ای برای معماری فراهم می آورد. در حالی که هندسه اقلیدسی ریشه در ابعاد و اندازه گیری داشته و در نتیجه به فضایی ملموس و قابل سنجش مرتبط می شود، هندسه تصویری با فضای بصری در ارتباط بوده و به درک از فضا بر می گردد. اوانز از به کارگیری هندسه تصویری در معماری دفاع می کند. او بیان می کند که تشخیص دو گونه متفاوت هندسه به ما این توانایی را می دهد که درک کنیم چرا خلق آثار معماری امری خطیر و منحصر به فرد است: “به عنوان یک ساختار متریک که از لحاظ بصری مورد قضاوت قرار می گیرد، معماری یک گونه از مبحث هندسه را با نوعی دیگر از مبحث سنجش و ارزیابی ترکیب می کند. شاید این امر دلیل وجود سردرگمی ها و نابسامانی های پیرامون این موضوع می باشد” [۶, p.xxxiii]. توسعه مبحث هندسه ترسیمی از الزامات و نیازهای معماری نشات می گیرد. برونلسکی به عنوان یک معمار اصولی سازنده در زمینه پرسپکتیوها با استفاده از روش های تصویرسازی هندسی ارائه کرد. آلبرتی نتایج تحقیق خود در زمینه پرسپکتیو را به صورت یک مفهوم آموزشی خلاصه نمود. هندسه تصویری با گسترش استفاده از مفهوم نقاط گریز و شکل گیری ترسیمات با استفاده از پرسپکتیو ایجاد شد. اکنون بر طبق نظریه ایوانز با جستجو برای یافتن ارتباط میان تصویرسازی و معماری، روش های جدیدی برای طراحی معماری شکل می گیرند. تصویرسازی ها مابین اشیاء مختلف عمل کرده و به عنوان ارتباطات انتقالی در نظر گرفته می شوند. دیاگرامی که در تصویر ۹ مشاهده می کنید چهار نوع موضوع را به تصویر کشیده است: شیء طراحی شده، تصویرسازی قائم، پرسپکتیو و تجسمی از شیء به صورت ترکیب شده با نحوه دریافت ناظر. ایوانز این دیاگرام را به صورت یک چهارضلعی تدریس می کرد، به این ترتیب که مرکز دیاگرام حذف شده و تمام نسبت ها برابر در نظر گرفته می شدند. مسیرهای موجود میان موضوعات دوسویه هستند.

تصویر ۹: دیاگرام ارتباطات انتقالی در تصویرسازی

دیاگرام اوانز می تواند به صورت مدلی نمادین از پروسه های طراحی معماری قلمداد شود. هندسه مفهومی ذهنی و معماری حقیقتی تجسم یافته و قابل درک می باشد. این دیاگرام ارتباطات نمادین میان شیء معماری طراحی شده، تجسمی از شیء و ترسیمات را طبقه بندی می کند. “در ارتباط میان هندسه و معماری ما به گونه ای از دنیای درونی ذهن به دنیای خارج از آن وارد می شویم. بنابراین زمانی که با مفهوم هندسه در معماری و کاربرد اشکال هندسی در معماری سرو کار داریم، در واقع به مسیر یا دروازه ای میان ذهنیات و واقعیات پا می گذاریم” [۶, p.354].

چنین تعاملاتی میان حوزه های توضیح داده شده از طریق بیان چند مثال شرح داده می شوند. می توان گفت پرسپکتیو بر شیء طراحی شده اثرگذار است. نمونه کلاسیکی که نشان دهنده این امر می باشد، حیاط طاقدار ساختمان “Palazzo Spada” در رم است که توسط فرانچسکو بورومینی در سال ۱۶۳۵ طراحی شد (همانطور که در تصویر ۱۰ مشاهده می کنید)، پرسپکتیو ارائه شده جلوه بصری معمارانه ای از بنا را به نمایش می گذارد که در آن کم شدن ارتفاع ردیف ستون ها و شیب رو به بالای کف حیاط تصور یک گالری کشیده و طویل را در ذهن بیننده ایجاد می کند.

تصویر ۱۰: حیاط طاقدار ساختمان “Palazzo Spada”، رم، فرانچسکو بورومینی ۱۶۳۵ [۱۸]

یک نمونه دیگر را می توان در ساختمان “مرکز علوم فائنو” در ولفزبرگ، آلمان مشاهده کرد که توسط زاها حدید در سال ۲۰۰۵ ساخته شده است (تصویر ۱۱). تعامل مثبت میان پرسپکتیو و شیء طراحی شده غالبا در آثار زاها حدید دیده می شود.

تصویر ۱۱: مرکز علوم فانئو، ولفزبرگ، آلمان، ساخته شده توسط زاها حدید، ۲۰۰۵ [۱۹]

پرستون اسکات کوهن [۴] در پروژه های طراحی معماری خود مستقیما با روش تصویرسازی کار می کند. او با مطالعه نمونه های تاریخی به این نتیجه دست یافت که بر اساس اصول هارمونی و هماهنگی، ساختمان هایی که به صورت متقارن طراحی می شوند، برای خلق یک واقعیت بصری با استفاده از تصویرسازی های پرسپکتیوی از حالت اولیه خود خارج می شوند. کوهن روشی جدید برای انجام پروسه طراحی با استفاده از “ابزار پرسپکتیو” معرفی کرد. “پروسه تصویرسازی برگشت پذیر است: پرسپکتیوها می توانند برای دستیابی به اشیاء و موضوعات مورد استفاده قرار گیرند و برعکس [۱۶]. او به عنوان مثال کار خود را با پرسپکتیوی از یک شیء آغاز کرد. این پرسپکتیو سپس به عنوان یک تصویرسازی قائم از شیء مطرح شد که بعدا به وسیله آن نماهای دیگر و تصویر سه بعدی و نهایتا خود شیء تولید شد.

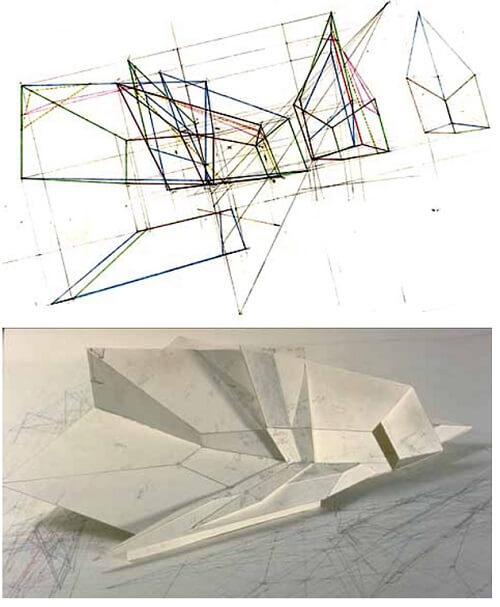تصویر ۱۲: الگوهایی برای مراکز آموزشی Head Start، ترسیمات و مدل سه بعدی، کوهن، ۱۹۹۴ [۱۶]

کوهن از روش تصویرسازی پرسپکتیوی برای خلق معماری استفاده می کند. ایده های او را می توان در دیاگرام ایوانز (تصویر ۹) در میان حوزه های ۳، ۴ و ۵ یافت. این یک نمونه جدید و جالب از طراحی معماریست که در آن هندسه پروسه طراحی را بر اساس ایده تصویرسازی جلو می برد.

نمونه ای دیگر از چنین دروازه ای میان ذهن و حقیقت را می تواند در بعضی از آثار بن ون برکل و کارولین باس مشاهده کرد، زمانی که ایده های توپولوژیکی را در معماری به کار می برند. آن ها در جلد اول کتاب “حرکت” می نویسند: “شکلی نامعین یا یک مکعب – دیگر تفاوتی ندارد. (…) آیا شما جعبه ها را دوست دارید؟ مشکلی نیست، امروزه کفش های شما می تواند در یک جعبه یا یک ساک بسته بندی شود؛ شما می توانید ساک را نیز درون یک جعبه قرار دهید” [۲, p.221]. تغییر شکل از یک مکعب به یک فرم نامشخص ممکن است از طریق تقارن توپولوژیکی که در آن همبندی شیء بدون تغییر باقی می ماند، قابل درک باشد. به عنوان مثال در خانه موبیوس، ایده نوار موبیوس[۱] نه به صورت تصویری بلکه به صورت مفهومی عامل پیش برنده پروسه طراحی می باشد؛ همان طور که برکل و باس در جلد دوم کتاب حرکت می نویسند: “مدل ریاضی نوار موبیوس عینا به فرم ساختمان تبدیل نشده است، بلکه درونمایه، مفهوم یا تجسمی از آن در محتوای معماری، مانند نورپردازی، پله ها و نحوه حرکت اشخاص در خانه به چشم می خورد” [۲, p.43].

تصویر ۱۳: کانسپت نوار موبیوس

تصویر ۱۴: خانه موبیوس، برکل، ۹۸-۱۹۹۳

نمونه های مطرح شده، روش های متنوعی از کاربرد هندسه و اشکال هندسی در معماری را در زمان کنونی نشان می دهد. به نظر می آید که ارتباطی مفید و موثر میان هندسه و معماری در گذشته و زمان حال وجود دارد، اگرچه در بعضی مواقع نقش هندسه تنها به عنوان مقوله ای قدیمی و تاریخی مورد توجه قرار گرفته است. با وجود این که معماری در عصر رنسانس از ریاضیات پیشی گرفت اما همچنان وارد شدن پیشرفت های جدید علم هندسه در معماری پروسه ای زمان بر خواهد بود. با این حال این پروسه از هم اکنون با یافتن تناسبات میان مفاهیم ریاضی هندسه انتقالی، هندسه تصویری، هندسه غیر اقلیدسی یا توپولوژی قرن نوزدهم میلادی با معماری آغاز می گردد. در این صورت ممکن است ارتباطی جدید و نیرومند میان هندسه و طراحی معماری شکل گیرد و مسئله کاربرد اشکال هندسی در معماری به درستی مورد توجه قرار گیرد.

5. نتایج

ارتباط میان طراحی معماری و هندسه با مفهوم هارمونی به عنوان اصلی حاکم بر تمام علوم و مخلوقات، آغاز می شود. آنالیزی بر دریافت های کهن از واژه هارمونی، ریشه هندسی و مفهوم برتر این کانسپت را برای تمام علوم و اصول طراحی روشن می سازد. امروزه علوم و رشته های هنری مختلف در بیشتر موارد به شدت از یکدیگر فاصله گرفته اند. به همین دلیل این خطر وجود دارد که ارتباط نیرومند موجود میان علم هندسه و معماری از بین برود. استیون هال، به عنوان کسی که هندسه و دیگر علوم را در آثار معماری خود به کار می برد، به این نکته توجه داشت: “به عنوان مثال یوهانس کپلر در کتاب اسرار گیتی شناسی، هنر، علم و کیهان شناسی را با یکدیگر ادغام کرده است. امروزه، تخصص گرایی باعث جدایی رشته های مختلف شده است؛ شکاف ها و فاصله های ایجاد شده مانع از دست یابی به پتانسیل های موجود در تعامل میان علوم مختلف و رشد متقابل آن ها خواهد شد” [۸].

از طریق یادآوری ارتباطات تاریخی میان علم هندسه و طراحی معماری، ما نه تنها به حفظ پیشینه فرهنگی خود کمک می رسانیم بلکه قادر به درک مزایای ترکیب تفکر هندسی و طراحی معماری نیز خواهیم بود. با گنجاندن آزمون ها و تجربیاتی که سازه های هندسی را در طراحی به کار برده اند، در برنامه آموزشی رشته معماری، ما باید منعکس کننده این ارتباطات تاریخی باشیم و سعی کنیم زمینه های جدیدی برای طراحی بر مبنای قوانین هندسی در معماری فراهم نماییم. تنها تعداد کمی از نمونه های موجود در این زمینه در این مقاله مورد بررسی اجمالی قرار گرفت. تلاش های بیشتری برای بیان این موضوع با جزییات دقیق تر در آینده مورد نیاز خواهد بود تا این ارتباطات را به صورت تاریخی و تئوریک، از نقطه نظر علم هندسه و معماری مورد تجزیه و تحلیل قرار داده و همچنین آن را به صورت تجربی و عملی در روند آموزش طراحی معماری به کار بندد.

نویسنده : کورنلی لیوپلد ، دانشگاه Kaiserslautern، آلمان

درباره نویسنده

کورنلی لیوپلد در رشته ریاضیات و فلسفه تحصیل کرد. او سخنران و مدرس ارشد هندسه تصویری و پرسپکتیو در دانشکده معماری، طراحی محیطی و منطقه ای و مهندسی عمران دانشگاه Kaiserslautern، در آلمان می باشد. موضوعات تحقیقاتی مورد علاقه او: هندسه تصویری و رسانه های جدید، مفاهیم فضایی هندسی و معماری، تجسم معماری، توسعه قابلیت های بصری فضایی، هندسه و طراحی معماری، کاربرد اشکال هندسی در معماری می باشد. تماس با نویسنده از طریق ایمیل: leopold@rhrk.uni-kl.de، تلفن: +۴۹-۶۳۱-۲۰۵-۲۹۴۱، فکس: +۴۹-۶۳۱-۲۰۵-۴۵۱۰، یا از طریق آدرس پستی:

University of Kaiserslautern / P.O. Box 3049 / D-67653 Kaiserslautern / Germany

و وبسایت:

http://www.uni-kl.de/AG-Leopold

امکان پذیر است.

---

ترجمه : فاطمه ناصری، کارشناسی ارشد تکنولوژی معماری گرایش دیجیتال (دانشگاه تهران)

لینک دانلود مقاله اصلی

REFERENCES

۱)[ps2id id=’1′ target=”/] Alberti, Leon Battista: The Ten Books of Architecture. Dover Publications, NewYork, 1987.

۲)[ps2id id=’2′ target=”/] Berkel, Ben van, Caroline Bos: Move. UNStudio Amsterdam, 1999.

۳)[ps2id id=’3′ target=”/] Bill, Max: Struktur als Kunst? Kunst als Stuktur? In: Georg Braziller: Struktur in Kunst und Wisssenschaft. Éditions de laConnaissance, Brüssel, 1967.

۴)[ps2id id=’4′ target=”/] Cohen, Preston Scott: Contested Symmetries and other predicaments in architecture. Princeton Architectural Press, New York, 2001.

۵)[ps2id id=’5′ target=”/] Corbusier, Le: Der Modulor. Deutsche Verlags-Anstalt, Stuttgart 1956, 7th ed.1998.

۶)[ps2id id=’6′ target=”/] Evans, Robin: The Projective Cast. Architecture and Its Three Geometries. The MIT Press, Cambridge, Massachusetts, 1995.

۷)[ps2id id=’7′ target=”/] Fuller, R. B..: Synergetics. 606.01. http://www.rwgrayprojects.com/synergetics

http://www.boontwerpt.nl/images/jpg/220buckmfuller.jpg

۸)[ps2id id=’8′ target=”/] Holl, Steven: Parallax. Birkhaeuser Basel, Boston, Berlin, 2000.

۹)[ps2id id=’9′ target=”/]Ivins, William M.: Art and Geometry. A Study in Space Intuitions. Dover Publications, New York, 1964 (Reprint of 1946).

۱۰)[ps2id id=’10’ target=”/] Kepler, Johannes: Weltharmonik (Harmonices mundi, (1619). R. Oldenburg Verlag, München, 1997.

۱۱)[ps2id id=’11’ target=”/] Leopold, Cornelie: Experiments on Relations between Geometry, Architecture and Music. Journal for Geometry and Graphics. Volume 9, Number 2, 2005 p.169-176.

۱۲)[ps2id id=’12’ target=”/] Leopold, Cornelie: Geometrische Strukturen. Exhibition of student’s works at University of Kaiserslautern, 2005.

۱۳)[ps2id id=’13’ target=”/] Naredi-Rainer, Paul v.: Architektur und Harmonie. Zahl, Maß und Proportion in der abendländischen Baukunst. Du Mont Buchverlag, Köln, 1982.

۱۴)[ps2id id=’14’ target=”/] Scriba, Christoph J., Peter Schreiber: 5000 Jahre Geometrie. Springer Verlag, Berlin, Heidelberg, New York, 2000.

۱۵)[ps2id id=’15’ target=”/] Vitruv: Zehn Bücher über Architektur. 3^rd edition, Wissenschaftliche Buchgesellschaft, Darmstadt, 1981.

۱۶)[ps2id id=’16’ target=”/] www.appendx.org/issue3/cohen/index.htm

۱۷)[ps2id id=’17’ target=”/] www.industrialorigami.com

۱۸)[ps2id id=’18’ target=”/] www.wikipedia.org

۱۹)[ps2id id=’19’ target=”/]www.wolfsburg-citytour.de/Museen/Phaeno_Museum_1/phaeno_museum_1.html

سطحی هندسی با یک ضلع پیوسته که از طریق پیچش ۱۸۰ درجه یک مستطیل باریک و بلند ایجاد می گردد. (مترجم)