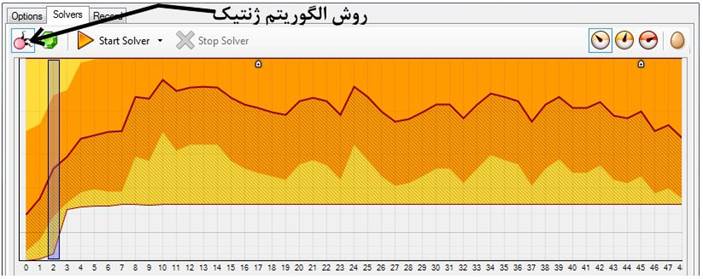استفاده از روش های تکاملی برای حل مسئله

با توجه به نکات گفته شده در مورد طبیعت به عنوان معلمی که توانسته است پس از گذشت میلیون ها سال کلکسیونی از فرم های بهینه از نظر پارامترهای حاکم بر خود را ارائه دهد می توان به جستجوی ابزارهایی پرداخت که بتوان بوسیله ی آن فاصله ی ایجاد شده بین سازه، معماری، تاسیسات و محیط پیرامون را کاهش داد. این ابزار باید بدون شک در روش هایی که طبیعت از آن ها برای بهینه شدن استفاده می کند ریشه داشته باشد. در اولین گام روش های بهینه سازی تکاملی که سال هاست در علوم کامپیوتر برای بهینه سازی مسائل چند پارامتری استفاده می شود به عنوان ابزار مناسب این کار دیده می شود.

روش های تکاملی حل مسئله و یا الگوریتم ژنتیک روش هایی هستند که از اوایل سال  ۱۹۶۰ تعریف شدند. اولین بارقه های کشف چنین روش هایی موقعی بوده است که Lawrence J. Fogel  مقاله ای بنیادین به اسم “سازماندهی فهم” را منتشر کرد که باعث شد اولین تلاش ها برای ورود به محاسبات تکاملی صورت گیرد. در اوایل ۱۹۷۰ با معرفی کارهای افرادی مثل Ingo Rechenberg و John Henry Holland شالوده ی روش های تکاملی حل مسئله ریخته شد. در حقیقت محاسبات تکاملی زمانی در تخصص برنامه نویسی وارد شد که Richard Dawkin کتاب “ساعت ساز کور”   را منتشر  کرد. این کتاب به همراه یک برنامه کوچک بود که یک سری اشکال پیچیده را بوسیله انتخاب شخص و جهش قوانین حاکم بر آن تولید می کرد. با گسترش کاربرد کامپیوتر در زندگی افراد و تخصص های غیر از بیولوژی امکان استفاده از روش های تکاملی برای حل مسئله های جدید بوجود آمد.(۳)

قبل از ورود به روش های تکاملی لازم است که نقص های آن عنوان شود تا نتیجه ای که از این روش حل مسئله بدست خواهد آمد بیشتر قابل درک باشد. از آنجایی که ما در دنیای ایده آل زندگی نمی کنیم تعریف کردن “بهترین راه حل” معمولا ممکن نیست.  هر روشی محدودیت ها و مشکلات خاص خود را دارد. در مورد الگوریتم های تکاملی این محدودیت ها شناخته شده و قابل توجه اند و به همین دلیل برای حل بعضی مسائل مناسب نیستند. اول از همه الگوریتم های تکاملی کند هستند. بعضی از مسائل با این روش روز ها و یا حتی هفته ها ممکن است به طول بیانجامد. مخصوصا مسائلی که به صورت پیچیده با یکدیگر در ارتباطند. مثلا حل یک مسئله ی ساده ی مرتبط با سازه و فرم ممکن است هر گام آن یک دقیقه به طول بیانجامد. در صورتی که ما مثلا ۵۰ نسل پیشنهادی (جواب بهینه) را در خواست کنیم عملا حل مسئله به دو روز  خواهد کشید!

در گام دوم روش های تکاملی یک راه حل تضمین شده ارائه نمی دهند مگر اینکه یک بازه ی “به مقدار کافی مناسب” برای آن تعریف گردد. این بدین معنی است که روش های تکاملی باید یک تابع هدف داشته باشند تا اجرا شوند. با این همه روش های تکاملی مزایایی نیز دارند که آن را از دیگر روش های حل مسئله قوی تر جلوه می دهند. روش های تکاملی منعطف بوده و برای بازه ی متنوعی از مسائل قابل استفاده هستند. برای مثال مسائلی که با روش های حل مسئله ی خاصی بسیار تودرتو و پیچیده به نظر می آیند توسط روش های تکاملی سریع تر به جواب های قابل قبول دست خواهد یافت. یک مزیت مهمی که روش های تکاملی دارند این است که مسائل پیچیده را ساده تر کرده و مسائلی که دارای محدودیت های بیش از حد باشند را با اصلاح هایی سریع تر حل می کنند. در ادامه چون این روش ها پیشرفت کننده هستند هر زمان می توان جواب های میانه را نیز استخراج کرد. در ادامه روش های تکاملی در هر مرحله تعدادی جواب بهینه را ارائه داده و در مرحله ی بعد جواب های با کیفیت بهتر از مرحله ی قبل را ارائه می دهند.این مسئله باعث می شود که در صورت قطع عملیات در میانه ی راه حل به جواب هایی دست یابیم که نسبتا بهینه اند. این بدین معنی است که هر مرحله که این روش به جلو می رود جواب های استخراجی بهتری بدست خواهد آمد. در انتها روش های تکاملی دارای انعطاف بالایی هستند. بدلیل اینکه پروسه ی حل مسئله قابل مشاهده است کاربر می تواند با تغییر در آن توانایی های آن را افزایش داده و یا قسمتی خاص از بازه ی حل مسئله را مورد بررسی قرار دهد.

پروسه ی حل مسئله

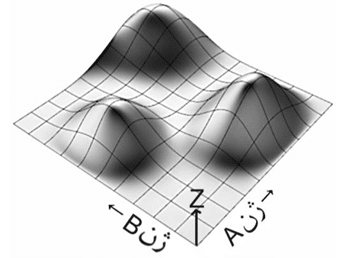
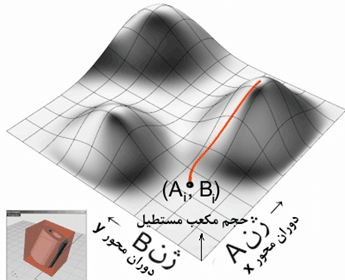
در شکل (۱۲) یک سطح برازش شده بر اساس متغییر های موجود (A و B ) نشان داده شده است. دو متغییر تولید کننده ی این سطح بوسیله ی یک تابعی Z را تولید می کنند (Z=f(A,B))  که در مسئله ی ما ناشناخته است. در صورتی که تابع f برای تمامی نقاط مشخص باشد بوسیله محاسبات ریاضی مانند مشتقات جزئی می توان نقاط ماکزیمم سطح را بدست آورد. بدلیل ناشناخته بودن تابع تولید کننده ی سطح هدف مسئله پیدا کردن نقاط ماکزیمم سطح (بر اساس تابع هدف) است. برای حل مسئله بوسیله ی روش های تکاملی به هر یک از پارامترها ژن اتلاق می شود. با تغییر ژن A ممکن است تابع نتیجه بر اساس خواسته ی ما بهتر و یا بدتر شود. درنتیجه با تغییر ژن A نقطه ی برازش شده بر روی سطح بالا و یا پایین می رود. ولی برای هر مقدار A می توانیم مقدار B را نیز تغییر داده و مجددا نقاط برازش بر اساس خواسته ی ما بهتر و یا بدتر شود. برای هر ترکیبی از A و B مقداری بر روی سطح برازش می شود که در عمل مقدار ارتفاع (Z) سطح است. وظیفه ی حل کننده پیدا کردن مرتفع ترین نقطه سطح است.

شکل(۱۲) سطح برازش شده (Z) بر اساس دو ژن(پارامتر) A و B و بوسیله ی تابع ناشناخته ی f

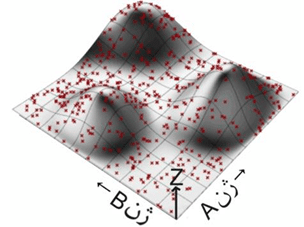
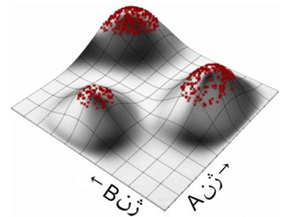
مطمئنا خیلی از مسائل نه با دو ژن بلکه با ژن های متعدد تعریف خواهند شد و در این مورد دیگر نمی توان از مثال ملموس سطح برازش شده استفاده کرد. یک مدل با ۱۲ ژن یک حجم انتزاعی ۱۲ بعدی برازش شده در یک فضای ۱۳ بعدی خواهد بود! بدلیل اینکه ژن های یک بعدی و دو بعدی ملموس ترند در ادامه با همین محدودیت اصول روش های تکاملی شرح داده خواهد شد و باید توجه داشت که هنگامی که از سطح برازش شده صحبت می شود ممکن است منظور چیزی خیلی پیچیده تر از تصاویر نشان داده شده باشد. با شروع الگوریتم حل کننده ی مسئله از آنجایی که سطح برازش شده ناشناخته است الگوریتم ابتدا چند دسته راه حل را به صورت اتفاقی بر روی دامنه ی مسئله توزیع می کند. یک ژنوم چیزی نیست جز مقادیر مشخص شده برای هر یک از ژن ها (پارامتر ها). در مورد مثال بالا یک ژنوم می تواند برای مثال مقدار { ۰٫۲= A و ۰٫۵= B }  باشد. الگوریتم پس از تولید راه حل های تصادفی آن ها را بررسی کرده و مقدار برازش شده محاسبه می کند. در شکل (۱۳) نمونه ای از توزیع اولیه ی الگوریتم تکاملی نشان داده شده است. پس از اینکه مقدار هر یک از ژنوم ها بدست آمد(ارتفاع سطح در مورد مثال بالا) می توان لیستی از بهترین تا بدترین راه حل تولید شده را تولید کرد. ارز آنجایی که ما به دنبال مرتفع ترین نقطه هستیم منطقی است که ژنوم های با مقدار بیشتر به قله نزدیک ترند تا ژنوم های کوچک تر. در نتیجه می توان بدترین جواب های بدست آمده را از بین برد و بر روی جواب های بهتر تمرکز کرد. شکل (۱۴) انتخاب های بهتر با توجه به اولین نسل تولید شده نشان داده شده است.

(۱۳)

(۱۴)

شکل(۱۳) نقاط توزیع شده توسط الگوریتم تکاملی

شکل(۱۴) نقاط برگزیده از بین راه حل های تصادفی در مرحله ی اول

خروج از برنامه و استفاده ار جواب هایی که در اولین مرحله از اجرای الگوریتم بدست آمده است به حد کافی مفید نیست زیرا نسل اولیه به صورت تصادفی تولید شده است. عملیاتی که در مرحله ی بعد صورت می گیرد گسترش بهترین ژنوم ها برای تولید نسل بعدی خواهد بود. وقتی که دو ژنوم برگزیده با یکدیگر تریکب شوند و نسل جدیدی را تولید کنند نسل تولید شده در فضای میانه ی جواب ها خواهد بود و در نتیجه جواب های جدیدتری بررسی خواهد شد. در شکل (۱۵) این عملیات نشان داده شده است.

شکل(۱۵) نقاط تولید شده توسط ترکیب دو ژنوم برگزیده

در این مرحله نسل جدیدی تولید شده است که کاملا تصادفی نیست و شروع به نزدیک شدن به سه نقطه ی ماکزیمم می کند. عملیات انجام شده به صورت یک الگوریتم تکرار پذیر با حذف بدترین گزینه ها و تولید نسل به کمک بهترین گزینه ها ادامه می یابد تا به نقاط ماکزیمم که عملا جواب مسئله هستند منتهی شود. در شکل (۱۶) انتهای پروسه ی الگوریتم تکاملی نشان داده شده است.

شکل(۱۶) رسیدن به نقاط ماکزیمم به عنوان جواب مسئله با تکرار عملیات الگوریتم تکاملی

انجام چنین عملیاتی نیاز به پنج قسمت مهم دارد که به آن آناتومی الگوریتم حل کننده ی مسئله مشهور است :

• تابع هدف
• مکانیزم انتخاب
• الگوریتم تزویج
• الگوریتم تلفیق
• کارخانه ی جهش

تابع هدف (Fitness function)

در دنیای طبیعت تابع هدف خاصی نمی توان تعریف کرد . معمولا گفتن اینکه دقیقا تابع هدف یک موجود چیست بسیار مشکل است. مطمئنا ارتباطی با اینکه موجود تبدیل به قوی ترین و یا سریعترین شود وجود ندارد. دلیل اینکه گیاه پیچک همانند درختان تنه ی قطور نمی سازد این است که پرداختن به افزایش قطر گیاه باعث کاهش انعطاف پذیری آن و در نتیجه غیر بهینه شدن فرآیند پیچیدن آن به دور دیگر گیاهان که لازمه ی دسترسی به نور است می شود. تابع هدف برآیند هزاران فاکتور های متناقض و متفاوت است. رسیدن به تابع هدف به کمک روش های تکاملی ایجاد سازش و برآورده کردن عادلانه ی این فاکتور هاست.

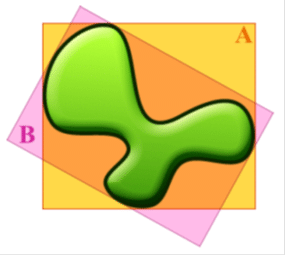
در روش های بهینه سازی تکاملی تعریف تابع هدف خیلی ساده تر صورت می گیرد. تابع هدف هر چیزی می تواند باشد، هر تابعی که ما بخواهیم. ما در تلاشیم که یک مسئله را حل کنیم و در نتیجه می توانیم تشخیص دهیم که هدف چیست. برای مثال تصور کنید که ما می خواهیم یک فرمی را با کمترین دور ریز مصالح بسازیم. می توان مسئله را به این صورت بیان کرد که تابع هدف یک مستطیل (در دو بعد) و یا یک مکعب مستطیل (در سه بعد)  می باشد که با کمترین اختلاف یک سطح  و یا یک حجمی را احاطه می کند. در شکل (۱۷) تابع هدف پیدا کردن مستطیلی است که کمترین مساحت را داشته و سطح دلخواه ارائه شده را بپوشاند. مطمئنا مستطیل B به دلیل داشتن مساحت کمتر نسبت به A بهینه تر است.

شکل(۱۷) تابع هدف با عنوان مستطیل احاطه کننده ی یک سطح که دارای کمترین مساحت باشد.

مستطیل B دارای مساحت کمتری نسبت به A بوده و در نتیجه بهینه تر است.

وقتی که هدف ساخت سه بعدی یک حجم باشد به نظر چرخاندن آن تا جایی که کمترین مصالح  مصرف شود یک راه حل خوب برای پیدا کردن بهینه ترین جواب مسئله است. برای چرخاندن یک مکعب مستطیل نیاز به سه محور دوران داریم تا تمامی حالات ممکن را بررسی کنیم. برای ملموس تر شدن مسئله دو دوران در راستای محور x و y نمایش داده می شود. در نتیجه ژن A معادل زاویه ی دوران محور x و ژن B معادل زاویه ی دوران محور y مکعب مستطیل احاطه کننده ی حجم است. از آنجایی که دوران بیش از ۳۶۰ درجه مفهومی ندارد بازه ی دوران محدود بوده و می توان آن را بین صفر تا ۹۰ درجه تعریف کرد. با دوران حول محور y می توان برای نمونه  جواب های نشان داده شده در شکل (۱۸) را تولید کرد.

شکل(۱۸) مکعب مستطیل احاطه کننده ی حجم با دوران حول محور y

در صورتی که زاویه ی دوران دلخواه برای هر یک از محور های دوران انتخاب کنیم در عمل یک نقطه با مختصات (Ai,Bi ) انتخاب کرده ایم که از یک طرف Ai معادل زاویه ی دوران حول محور x و Bi معادل زاویه ی دوران حول محور y می باشد. از طرف دیگر این مختصات را می توان متناظر نقطه ای واقع بر روی سطح تابع هدف دانست که برابر حجم مکعب مستطیل احاطه کننده ی فرم است (شکل (۱۹)).

شکل(۱۹) مجموعه ی دو محور دوران مکعب مستطیل احاطه کننده ی حجم را می توان معادل مختصاتی دانست که بر روی سطح معرف تابع هدف (حجم مکعب مستطیل) قرار دارد (Ai,Bi). ارتفاع این مختصات تعیین کننده ی جواب مسئله است.

با توجه به مثال زده شده و با پیگیری مراحل نشان داده شده در شکل (۱۲) الی (۱۶) می توان دو زاویه ی دوران که کمترین مصالح مصرفی که به عنوان تابع هدف مشخص شده بود را بدست آورد. انتخاب تابع هدف به عنوان اولین گام و تعیین کننده ترین فاکتور حل مسائل بهینه سازی است.

مکانیزم انتخاب (Selection Mechanism)

تکامل در طبیعت با انتخاب طبیعی صورت می گیرد. طبیعت با انتخاب بهترین نسل ها که عملا گزینه هایی هستند که تحت شرایط سخت طبیعی دوام آورده اند مدام در حال بهتر کردن نسل های بعدی است. اما این مسئله در رایانه به شکل ساده تری صورت می گیرد. تنها یک سوال است که باید پاسخ داده شود: از نظر تابع هدف گزینه ی مناسب برای تولید نسل بعدی کدام است؟

در ادامه  از برنامه ی Galapagos که ضمیمه ی نرم افزار معماری پارامتریک Grasshopper می باشد استفاده شده است. این نرم افزار  از روش های تکاملی برای حل مسئله استفاده می کند. در این نرم افزار در گام اول باید یک نسل مولد انتخاب شود تا نسل های بعدی از این نسل تولید شوند. در نوع انتخاب این نسل مولد می توان چند روش به کار برد که سه روش بیشترین کاربرد را دارد:

• انتخاب ایزوتروپیک و یا یکنواخت (Isotropic selection)

در این روش تمامی جواب ها ی برگزیده شانس یکسانی برای تاثیر بر روی نسل بعدی را دارند. این روش ساده ترین روش انتخاب بوده و از پیدا شدن جواب های بهینه ی محلی که عملا ممکن است بهترین جواب نباشند جلوگیری می کند. در شکل (۲۰) این روش انتخاب نشان داده شده است.

شکل(۲۰) روش انتخاب ایزوتروپیک (همگن) نسل های مولد

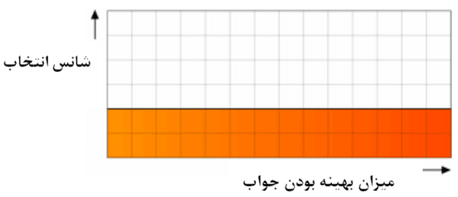
• انتخاب انحصاری (Exclusive selection)

در این روش با توجه به شکل (۲۱) فقط بخش مشخصی از گزینه های بهینه توانایی تولید نسل داشته و دیگر گزینه ها حذف می شوند.

شکل(۲۱) روش انتخاب انحصاری نسل های مولد

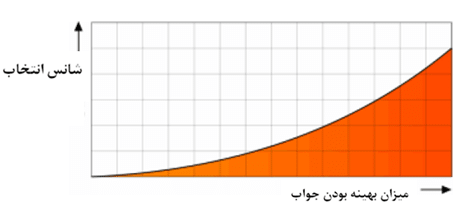
• انتخاب جهت دار (Biased selection)

در این روش با بهینه تر شدن جواب ها شانس انتخاب آن ها برای تولید نسل بعدی بیشتر خواهد شد. می توان با ضرب تابع خاصی در این روش شانس انتخاب را تشدید یا کاهش داد. در شکل (۲۲) این روش نشان داده شده است.

شکل(۲۲) روش انتخاب جهت دار نسل های مولد

الگوریتم تزویج (Coupling Algorithm)

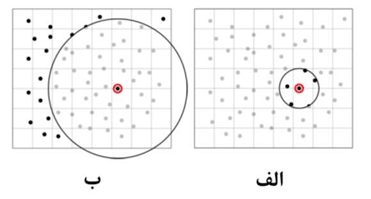
پس از انتخاب یک تعداد مشخص نسل اولیه و تولید آن ها توسط تابع هدف گام بعدی تزویج این نسل ها و تولید جواب های بعدی است. برای این کار نیاز به روش خاص تزویج نتایج است. یکی از این روش ها تزویج نتایج قرار گرفته در نزدیکی یکدیگر است. در دنیای طبیعی ازدواج موجود با ژن شبیه به خود باعث ایجاد ژن های معیوب ولی جهش یافته می شود. در دنیای کامپیوتر این عمل باعث کاهش تنوع در نتایج خواهد شد و در نتیجه احتمال یافتن اکسترمم های اصلی کاهش یافته و احتمال رسیدن به اکسترمم های محلی افزایش می یابد (شکل ۲۳- الف). روش دیگر، تزویج نتایج با جواب هایی است که از مقدار مشخص همسایگی دورترند. این روش در بعضی مواقع مناسب است ولی ممکن است به دلیل احتمال طی کردن مسیر متفاوت نسل های دورتر باعث اختلال در روش بهینه یابی شود(شکل ۲۳- ب).

شکل(۲۳)  تزویج نتایج با همسایگی مشخص (الف) ، تزویج نتایج بیرون از همسایگی مشخص

بهترین روش انتخاب نتایجی است که نه خیلی نزدیک و نه خیلی دور باشند. در این مورد احتمال رسیدن به نتایج بهینه بیشتر است. این روش در شکل (۲۴) نشان داده شده است.

شکل(۲۴)  تزویج نتایج با گزینه هایی که نه نزدیک و نه دور بوده و به صورت بازه تعریف می گردد

الگوریتم تلفیق (Coalescence Algorithm)

بعد از انتخاب مولد، نسل های بعدی باید بوسیله ی مکانیزمی تولید شود. در روش های تکاملی ژنوم ها همانند متغییر هایی عمل می کنند که بازه ی مشخصی دارند. برای تلفیق دو ژنوم (که دارای تعدادی مشخص ژن و یا در واقع متغییر هستند) باید تصمیم گرفته شود که کدام مقدار برای ژن های آن ها در نظر گرفته شود. برای این عمل چندین روش موجود است.

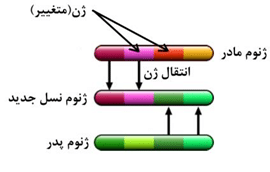
در روش دور رگه ای (crossover) همانند شکل (۲۵) درصدی از ژن های نسل جدید از نسل مادر به ارث برده می شود و ما بقی از پدر.

شکل(۲۵)  تلفیق به روش دورگه ای

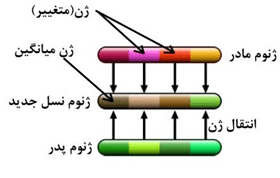
در روش اختلاطی میانگین دو ژن متناظر یکدیگر برای ژن نسل جدید در نظر گرفته می شود. این تلفیق در شکل (۲۶) نشان داده شده است.

شکل(۲۵)  تلفیق به روش اختلاطی (میانگین)

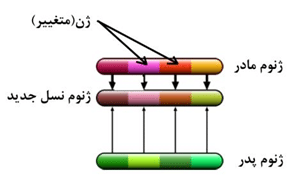
در این روش می توان در صورتی که به طور مثال ژنوم مادر بهینه تر از ژنوم پدر است ضریب تاثیر بیشتر از ۵۰% را برای آن در نظر گرفت. این عمل در شکل (۲۶) نشان داده شده است.

شکل(۲۵)  تلفیق به روش اختلاطی (دارای ضریب)

کارخانه ی جهش (Mutation Factory)

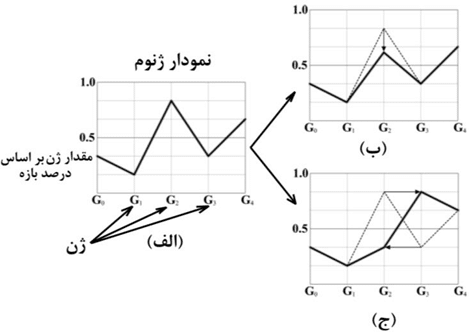
تمامی مکانیزم های تشریح شده تا به حال ( انتخاب، تزویج، تلفیق) به گونه ای طراحی شده اند که با هر پیشرفت در نسل جواب ها بهینه تر شوند. با این حال این مکانیزم ها تمایل دارند که تنوع در جواب حل مسئله را کاهش دهند. تنها مکانیزمی که می تواند تنوع در جواب ایجاد کند ایجاد جهش در ژنوم هاست. برای نشان دادن مکانیزم جهش می توان از نموداری استفاده کرد که ژن های یک ژنوم بر روی یک محور و مقدار هر ژن بر اساس بازه ای که می تواند اتخاذ کند بر روی محور دیگر نشان داده شود ( شکل (۲۶-الف)). متداولترین روش در مکانیزم جهش روش جهش نقطه ای (point mutation) می باشد که در شکل (۲۶- ب) نشان داده شده است. در این روش مقدار یک ژن را می توان به صورت انفرادی تغییر داد. روش دیگری نیز وجود دارد که کمتر متداول بوده و در آن مقادیر ژن های همسایه با یکدیگر جابجا می شود. این روش جهش معکوس (Inversion Mutation) می گویند (شکل (۲۶- ج)).

شکل(۲۶)  نمودار ژنوم با شماره ی ژن بر روی محور افق و مقدار ژن نسبت به بازه قابل اتخاذ بر روی محور عمود (الف) ، جهش نقطه ای با تغییر مقدار یک ژن (ب)، جهش معکوس با جابجایی مقادیر ژن های همسایه (ج)

مثال ۱ :  موقعیت یابی یک آتش نشانی با کمترین فاصله نسبت به مراکز شهری

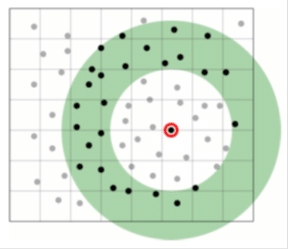
برای روشن تر شدن روش الگوریتم ژنتیک یک نمونه مسئله تشریح می شود. در این مسئله تعداد ۲۰ نقطه با مختصات مختلف مشخص شده اند (شکل (۲۷- الف)). این نقاط می تواند معرف مراکز شهری بوده که تابع هدف مسئله ترسیم دایره ای است که تمامی این نقاط را در بر بگیرد و در ضمن کمترین مساحت را اشغال کند. مرکز این دایره در واقع محل ساخت یک آتش نشانی می باشد که بتواند با کمترین فاصله به تمامی این مراکز شهری دسترسی داشته باشد. در این مسئله پارامترهای قابل تغییر مختصات مرکز ساختمان آتش نشانی به صورت (Xc,Yc)  و فاصله دسترسی به صورت شعاع دایره به صورت rc می باشد (شکل (۲۷ – ب)). در نتیجه برای حل این مسئله سه سه ژن (متغییر) قابل تعریف بوده و نرم افزار قادر است این پارامتر ها را تغییر دهد.

شکل(۲۷)  (الف) ۲۰ نقطه ی مشخص شده برای ترسیم دایره ای با کمترین شعاع، (ب) دایره های مختلف ترسیم شده

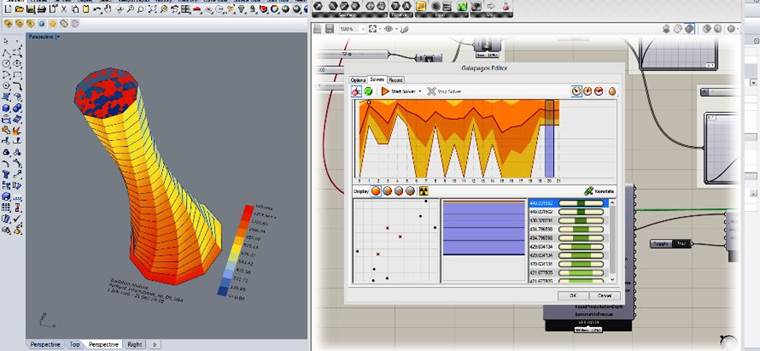
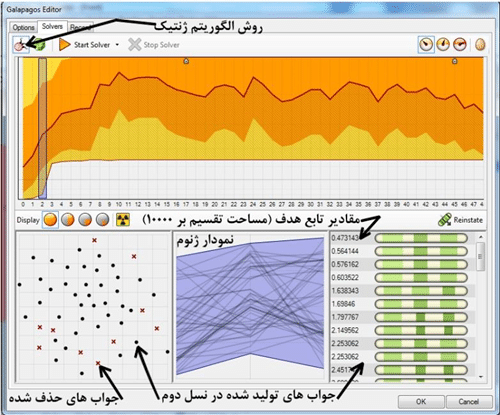
پس از اختصاص سه پارامتر معرفی شده به عنوان ژن به برنامه به علت احتمال دادن جواب های محلی و نرسیدن به جواب بهینه برنامه طوری تنظیم شد تا تعداد نسل های اولیه بیش از حد معمول باشند. در شکل (۲۸) کل عملیات انجام شده در نرم افزار Galapagos نشان داده شده و در شکل(۲۹) روند حل مسئله و در شکل (۳۰) جواب نهایی مسئله نیز مشخص شده است.

شکل(۲۸)  روند کامل حل مسئله در نرم افزار Galapagos، قسمت های مختلف نرم افزار نیز نشان داده شده است

شکل(۲۹)  روند بهینه سازی نرم افزار، در این تصویر چهار نمونه جواب برای نشان دادن اصلاح جواب ها توسط الگوریتم ژنتیک  انتخاب و نشان داده شده است

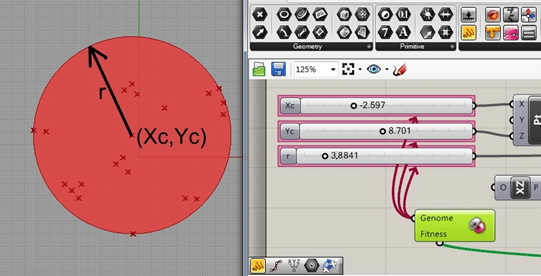
شکل(۳۰)  جواب بهینه ی بدست آمده توسط نرم افزار Grasshopper – Galapagos   با جانمایی ساختمان آتش نشانی به مختصات (-۲٫۵۹۷,۸٫۷۰۱) و شعاع  ۳٫۸۸۴۱ کیلو متر

مثال ۲ :  بهینه سازی یک برج فرضی (شرکت SOM)

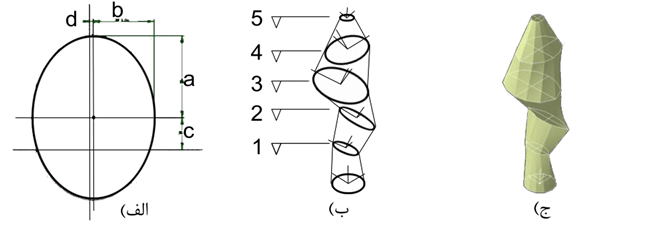
این مثال بهینه سازی یک برج فرضی با ارتفاع ۳۰۰ متر می باشد که تحت محدودیت های هندسی متفاوتی طراحی می شود(۵). این بهینه سازی با تابع هدف بیشترین دریافت انرژی خورشیدی توسط پوسته ی ساختمان تعریف شده است. ساخت این برج با هدف این بوده است که نمای ساختمان دارای سطوحی باشد که بر روی آن های سلول های خورشیدی نصب شده و بیشترین انرژی را برای ساختمان تامین کند. هندسه ی برج توسط ترکیبی از مختصات نقطه و طول مشخص خطوط کنترل شده است (شکل ۳۱). مقطع ساختمان در شش سطح ارتفاعی مشخص و برج بوسیله جاروب کردن سطحی که از این مقاطع عبور کند تعریف گردیده است. مقطع ساختمان در پلان تغییر نکرده و دارای هندسه ی ثابتی می باشد. پنج مقطع دیگر برج توسط یک بیضی تعریف گردیدند که از مرکز این بیضی توسط پارامتر های انحراف داشته باشد (شکل ۳۱ – الف). این انحراف دارای بازه ی خاصی بوده و همچنین بیضی تعریف شده نیز از مقدار مشخصی کوچک تر و یا بزرگ تر نمی باشد.

شکل(۳۱)  روند ساخت برج، (الف) تعریف چهار پارامتر برای تعریف مرکز بیضی برای هر طبقه، (ب) پنج مقطع از برج که قابلیت تغییر در پارامتر های چهارگانه ی آن ها وجود دارد، (ج) برج با جاروب کردن سطحی که از پلان و پنج مقطع مشخص شده عبور می کند تعریف می گردد

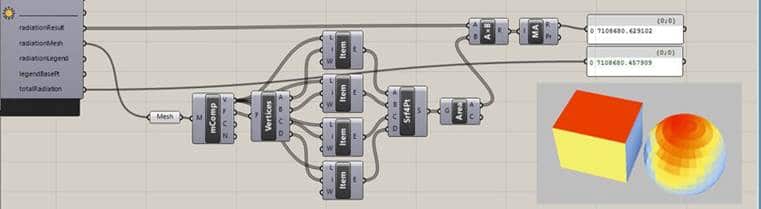
با توجه به مسئله ی تعریف شده، برای ساخت سطح برج ۲۰ پارامتر متفاوت باید تعریف گردد ( هر ۵ طبقه ی متغییر دارای ۴ پارامتر می باشد). تابع هدف ترکیبی از ماکزیمم مساحت کف طبقه و ماکزیمم سطح پوششی می باشد.  برای این مسئله ابتدا توسط الگوریتم ژنتیک ۷۵ حالت مختلف که هر حالت به صورت مجموع ۲۰ پارامتر تولید کننده ی سطح تعریف گردیده است تولید گردید. این عملیات ۷۵ برج مختلف را تولید کرده و پس از هر تولید سطح، برج مورد نظر در نرم افزار Ecotect برای مقدار تابش مورد بررسی قرار گرفته است. در کنار این عملیات مجموع سطوح طبقات و سطح پوشش برج نیز محاسبه گردیده است. پس از مشخص کردن امتیاز مورد نظر برای هر یک از پارامتر های میزان تابش، مساحت سطح و ممجموع مساحت کف طبقات نرم افزار مراحل بعدی را مورد بررسی قرار داده و همانند روند تعریف شده در الگوریتم ژنتیک جواب ها بدست آمده اند.

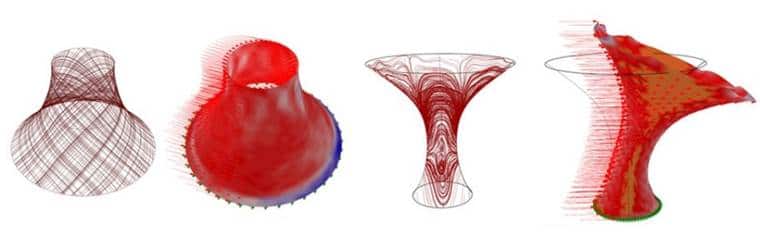
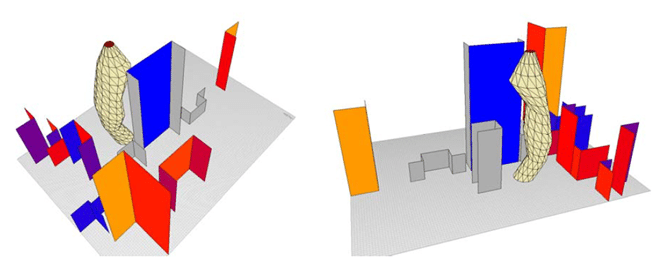
الگوریتم ژنتیک برای دو حالت خاص و با استفاده از داده های آب و هوای لاس وگاس(Las Vegas) اجرا شده است. در حالت اول برج بدون بافت شهری بررسی گردید تا فرم ساختمان تنها بر اساس تابش خورشید تولید گردد. جالب توجه می باشد که با  اینکه حرکت خورشید به صورت متقارن می باشد ولی جواب مورد نظر یک برج متقارن نبوده است (شکل ۳۲). در حالت دوم برج با بافت پیرامون مورد بررسی قرار گرفته است تا سایه ی ساختمان های مجاور بر روی برج در تمامی روز های سال و در ساعات مختلف روز بررسی گردد(شکل ۳۳). در شکل (۳۴) جایگاه قرار گیری برج در سایت نمایش داده شده است.

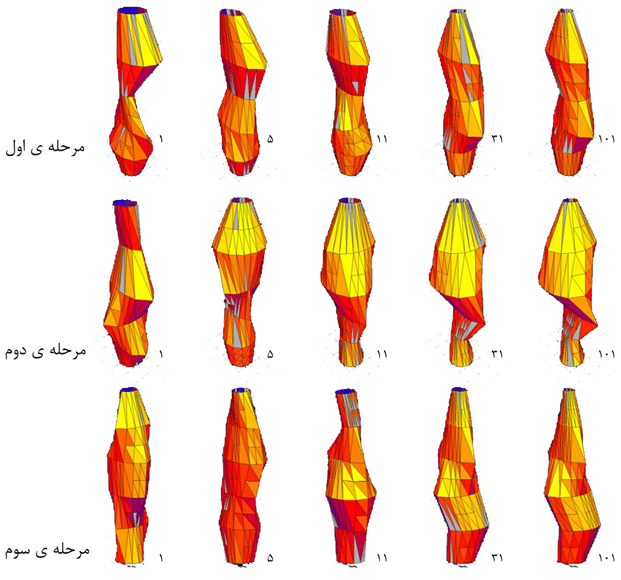
شکل(۳۲)  اعمال الگوریتم ژنتیک بر روی برج بدون در نظر گرفتن بافت محیط آن و با آب و هوای لاس وگاس، مرحله ی اول) جواب های شماره  ۱، ۵، ۱۱ ، ۳۱ و ۱۰۱ از روند الگوریتم ژنتیک و میزان تابش دریافتی هر یک، مرحله ی دوم) همان شماره جواب ها در مرحله ی دوم بهینه سازی، مرحله ی سوم) شماره جواب های قبلی در مرحله سوم الگوریتم ژنتیک

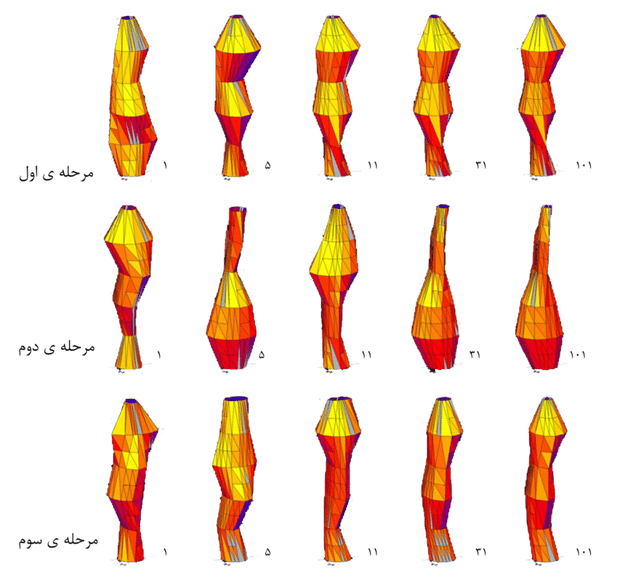
شکل(۳۳)  اعمال الگوریتم ژنتیک بر روی برج با در نظر گرفتن سایه ی ساختمان های پیرامونی و با آب و هوای لاس وگاس، مرحله ی اول) جواب های شماره  ۱، ۵، ۱۱ ، ۳۱ و ۱۰۱ از روند الگوریتم ژنتیک و میزان تابش دریافتی هر یک، مرحله ی دوم) همان شماره جواب ها در مرحله ی دوم بهینه سازی، مرحله ی سوم) شماره جواب های قبلی در مرحله سوم الگوریتم ژنتیک

بهینه سازی برج در سه مرحله (چه بدون بافت و چه با حضور بافت پیرامون) همگرا بوده و مرحله ی سوم  نسبت به مرحله ی اول بررسی برای حالت بدون بافت ۶ درصد و برای حالت بافت پیرامون ۱۲ درصد افزایش یافته است. جواب های بدست آمده نسبت به یک برج استوانه ای برای حالت بدون بافت ۲۱ درصد و برای حالت بافت پیرامون ۲۷ درصد افزایش تابش را به همراه دارد. در تیجه الگوریتم ژنتیک در هر دو حالت جوا ب های مناسب تری نسبت به یک برج استوانه ای بدست آورده است.

شکل(۳۴)  موقعیت برج در سایت برای بررسی فرمی که بیشترین تابش را دریافت می کند

منابع

• http://en.wikipedia.org/wiki/Morphology_(biology)
• Performance-oriented Architecture :Towards a Biological Paradigm for Architectural Design and the Built Environment, Michael U. Hensel, FORMakademisk, 3 Nr.1 2010, 36-56
• http://en.wikipedia.org/wiki/Interactive_evolutionary_computation
• Evolutionary Principles applied to Problem Solving – Grasshopper, http://www.grasshopper3d.com/profiles/blogs/evoutionary-principles
• Architectural Genomics, Keith Besserud, AIA, Skidmore, Owings, & Merrill LLP

نویسنده : محمد یزدی کارشناسی ارشد تکنولوژی معماری از دانشگاه تهران